List of moments of inertia
The following is a list of moments of inertia. Mass moments of inertia have units of dimension mass × length2. It is the rotational analogue to mass. It should not be confused with the second moment of area (area moment of inertia), which is used in bending calculations.
The following moments of inertia assume constant density throughout the object, and the axis of rotation is taken to be through the center of mass, unless otherwise specified.
| Description | Figure | Moment(s) of inertia | Comment |
|---|---|---|---|
| Point mass m at a distance r from the axis of rotation. | 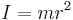 |
— | |
Two point masses, M and m, with reduced mass  and separated by a distance, x. and separated by a distance, x. |
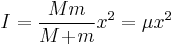 |
— | |
| Rod of length L and mass m (Axis of rotation at the end of the rod) |
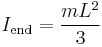 [1] [1] |
This expression assumes that the rod is an infinitely thin (but rigid) wire. This is also a special case of the thin rectangular plate with axis of rotation at the end of the plate, with h = L and w = 0. | |
| Rod of length L and mass m | 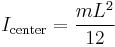 [1] [1] |
This expression assumes that the rod is an infinitely thin (but rigid) wire. This is a special case of the thin rectangular plate with axis of rotation at the center of the plate, with w = L and h = 0. | |
| Thin circular hoop of radius r and mass m | 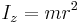 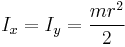 |
This is a special case of a torus for b=0. (See below.), as well as of a thick-walled cylindrical tube with open ends, with r1=r2 and h=0. | |
| Thin, solid disk of radius r and mass m | 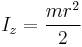 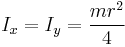 |
This is a special case of the solid cylinder, with h=0. | |
| Thin cylindrical shell with open ends, of radius r and mass m | 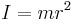 [1] [1] |
This expression assumes the shell thickness is negligible. It is a special case of the thick-walled cylindrical tube for r1=r2.
Also, a point mass (m) at the end of a rod of length r has this same moment of inertia and the value r is called the radius of gyration. |
|
| Solid cylinder of radius r, height h and mass m | 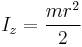 [1] [1]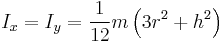 |
This is a special case of the thick-walled cylindrical tube, with r1=0. (Note: X-Y axis should be swapped for a standard right handed frame) | |
| Thick-walled cylindrical tube with open ends, of inner radius r1, outer radius r2, length h and mass m | 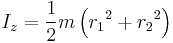 [1][2] [1][2]![I_x = I_y = \frac{1}{12} m\left[3\left({r_2}^2 %2B {r_1}^2\right)%2Bh^2\right]](/2012-wikipedia_en_all_nopic_01_2012/I/3b287e5226f4bb01de7a7a3066f4202a.png) or when defining the normalized thickness tn = t/r and letting r = r2, then 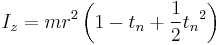 |
With a density of ρ and the same geometry 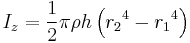 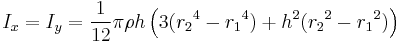 |
|
| Sphere (hollow) of radius r and mass m | 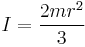 [1] [1] |
A hollow sphere can be taken to be made up of two stacks of infinitesimally thin, circular hoops, where the radius differs from 0 to r (or a single stack, , where the radius differs from -r to r). | |
| Ball (solid) of radius r and mass m | 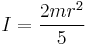 [1] [1] |
A sphere can be taken to be made up of two stacks of infinitesimally thin, solid discs, where the radius differs from 0 to r (or a single stack, where the radius differs from -r to r).
Also, it can be taken to be made up of infinitesimally thin, hollow spheres, where the radius differs from 0 to r. |
|
| Right circular cone with radius r, height h and mass m | 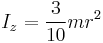 [3] [3]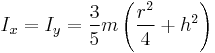 [3] [3] |
— | |
| Torus of tube radius a, cross-sectional radius b and mass m. | About a diameter: 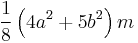 [4] [4]About the vertical axis: |
— | |
| Ellipsoid (solid) of semiaxes a, b, and c with axis of rotation a and mass m | 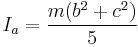 |
— | |
| Thin rectangular plate of height h and of width w and mass m (Axis of rotation at the end of the plate) |
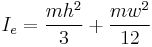 |
— | |
| Thin rectangular plate of height h and of width w and mass m | 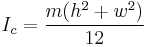 [1] [1] |
— | |
| Solid cuboid of height h, width w, and depth d, and mass m | 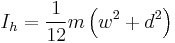 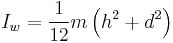 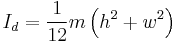 |
For a similarly oriented cube with sides of length  , , 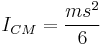 . . |
|
| Solid cuboid of height D, width W, and length L, and mass m with the longest diagonal as the axis. | 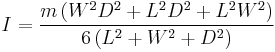 |
For a cube with sides  , , 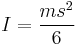 . . |
|
Plane polygon with vertices 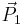 , , 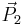 , , 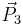 , ..., , ..., 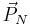 and and
mass |
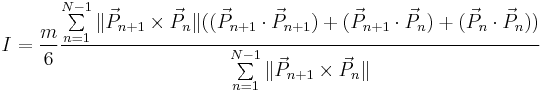 |
This expression assumes that the polygon is star-shaped. The vectors 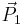 , , 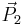 , , 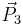 , ..., , ..., 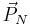 are position vectors of the vertices. are position vectors of the vertices. |
|
| Infinite disk with mass normally distributed on two axes around the axis of rotation
(i.e. |
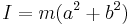 |
— |
See also
- Parallel axis theorem
- Perpendicular axis theorem
- List of area moments of inertia
- List of moment of inertia tensors
References
- ^ a b c d e f g h Raymond A. Serway (1986). Physics for Scientists and Engineers, second ed.. Saunders College Publishing. p. 202. ISBN 0-03-004534-7.
- ^ Classical Mechanics - Moment of inertia of a uniform hollow cylinder. LivePhysics.com. Retrieved on 2008-01-31.
- ^ a b Ferdinand P. Beer and E. Russell Johnston, Jr (1984). Vector Mechanics for Engineers, fourth ed.. McGraw-Hill. p. 911. ISBN 0-07-004389-2.
- ^ a b Eric W. Weisstein. "Moment of Inertia — Ring". Wolfram Research. http://scienceworld.wolfram.com/physics/MomentofInertiaRing.html. Retrieved 2010-03-25.
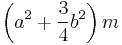
 uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.
uniformly distributed on its interior, rotating about an axis perpendicular to the plane and passing through the origin.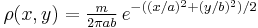 Where :
Where : 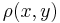 is the mass-density as a function of x and y).
is the mass-density as a function of x and y).